I found this fractal, when considering the interference of waves on the surface of the river. The wave is moving to the coast, is recognized and imposed on itself. Is there a specific order in those patterns that are created by waves? Let us try to find it. Let's not consider the entire wave, but only part of it - the motion vector of the wave. Will reflect the wave of "coast". We will make the flat coast - for the sake of simplicity of the experiment.


Take a rectangle with sides q and p. Send the vector from one corner. Vector comes to the side of the rectangle is reflected and moves to the next side. This continues until the vector does not fall into one of the remaining corners. If the size of the parties q and p - are relatively prime, it turns pattern (as we shall see later - fractal).

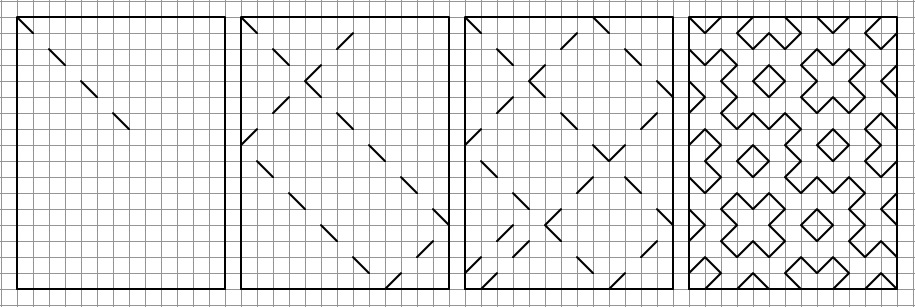
In the picture we see clearly the effect of this algorithm. Gif-animation: The most striking thing is that at different sides q and p we get a completely different fractals: Why do I call these patterns fractals? If you significantly increase the size of the parties q and p - it is clear that these patterns have the properties of self-similarity.

Increase will be very artful way. Take for example the pattern of 17x29. The following patterns are: 29x(17+29=46), 46x(29+46=75) ...
One side: a(n);
The second side: a(n+1)=a(n)+a(n-1);
17, 29, 46, 75, 121, 196, 317, 513, 830, 1343
As the Fibonacci numbers, only with other members of the first F(0)=17 and second F(1)=29.
clickable: I'll try to explain what's going on.
Let's separate from our rectangle piece. Square. Let's see what happens at the boundary of the square. Vector goes into that same point, from which came.
The number of cells through which will pass vector - always even number. Our square complements fractal that appears in the rectangle. New rectangle contains part of the fractal.
If separated from the fractal squares as many times as possible - get to the seed of fractal.

Results.
Chaos - it is also the order (fractal order). With their laws. Chaos has not been studied, but it is amenable to study. And all the desire of science - to detect these patterns. And ultimately connect pieces of the puzzle to see the big picture.

Let's take a look at the surface of the river. If you throw a stone at her - will wave. Circles, it is amenable to study. Speed, the period, wave length - this can be calculated all. But until then, until the wave reaches the shore, reflected and begins to overlap itself. Obtain chaos ( interference ), which is already difficult to study.
What if we move from the back? Simplify the behavior of waves on as much as possible. Simplify, find a pattern and then try to describe the already full picture.
What can be easier? Obviously, to make the reflective surface straight, without bending. Further, instead of the wave, to use only the motion vector of the wave. In principle, it is enough to construct a simple algorithm and simulated process on the computer. And even enough to make a "model" behavior of waves on a piece of paper in the cage.
What is the outcome? As a result, we see that the wave processes (that is, the ripples on the surface of the river), not chaos, but the imposition of fractals (self-similar structures) on each other.

Consider another kind of waves. As we known, the electromagnetic wave consists of three vectors - the wave vector and the vector of the electric and magnetic fields. As you can see, if the " catch" a wave in the closed area - where these vectors intersect, we get quite clear closed structures. It may be that the elementary particles - such as fractals?

The most common number, if you combine them with the help of elementary algorithms - generate the most unusual fractals. The most amazing thing is where the last thing we're looking for.